Beat Your Grandma at Cards - Chapter 6 - Perfect Information AIs
One of the most fundamental algorithms in AI is Minimax. In this article, we’ll describe how the seminal algorithm works, and give some in-depth examples. We’ll discuss a scenario with “Perfect Information”, meaning the AI knows everyone’s cards. Obviously, if a player could do this, it would be cheating, so it’s unacceptable for a real world AI, but it’s a good place to start, and it’s a necessary step for attaining a high quality non-cheating AI.
“Scoring” a Game’s State
The first step in Minimax is “scoring” a game state, meaning, assigning some point value to any given situation. This can usually be derived from actual tactics that we, as humans, might employ during a game. Think of a two player game you’ve played in the past. Could be chess, checkers, tic-tac-toe, or pretty much any game that comes to mind. In all of these games, you can probably imagine a way of giving a rough score to each player at any point in the game. For instance, in chess, if you have valuable pieces, like a queen or a rook, then you have a higher score. In checkers, if you have more kings, or you’ve lost fewer pieces, then you have a higher score. And in tic-tac-toe, if you have two in a row, or if you have unblocked rows or columns, then you have a higher score.
Who is in a better position?
For our Euchre AI, we’ll use the number of tricks your team has won. Having more tricks is a simple, objective way to tell if a team is doing better at any given moment. We could get much more complicated, like we could put values on each card and score teams higher if they own right or left bauers, or aces. Or we could score teams higher if the game is mid-trick and they’re currently winning a trick. These are all valid investigations, but every subtle change to the scoring can lead to massive butterfly effects in the overall strategy of the AI, so I like to keep my scoring simple and uncontroversial. Once you’ve developed your core AI, I encourage you to go buck wild with your scoring algorithm. A good scoring algorithm can boost an AIs performance significantly, and AIs with different scoring algorithms can be pitted against one another in a virtual coliseum to determine which one is better!
Pitting AIs against one another can be a nasty business
Once you’ve developed a scoring system, you might imagine an AI that “maximizes” this score. On any given turn, the AI would simulate every possible move, and choose the move that results in the highest score. Simple, right? Let’s call this hypothetical algorithm “maximax”.
Would Maximax Work?
However, maximax has a fatal flaw. Let’s illustrate with an example:
Consider this situation. It’s East’s turn, the game is tied at 1:1, and trump is diamonds. East has the ten of diamonds and the left bauer, and she’s short suited in clubs, so she can trump. If East was using maximax, she would most certainly play the left bauer in order to win the trick. It’s actually not a bad play at first glance, and lots of players might make it (especially if they’re not paying attention to who still has trump). It’s a play that I would probably make against my grandma.
But this is the type of play that separates the grandmas from the wannabe grandson whippersnappers.
Any grandma would know that playing the left bauer and winning the trick is not the winning play. The winning play is to discard the ace and lose the trick! This puts North on the offensive, and East can beat whatever he plays, and then East will still have the winning card.
In other words, playing the left bauer here will win this trick, but lose the next two tricks, whereas playing the ace will lose this trick, but win the next two tricks. This is completely counter-intuitive at first. How is losing an ace AND losing the trick the best play!?!?
This is the underlying fallacy of our hypothetical Maximax algorithm. You optimize near-term small gains, potentially at the cost of a grand strategic vision. We need a system that not only takes into account the score of each move, but also takes into account the eventual long-term outcomes of each move.
Minimax’s Solution
In order to reveal how minimax solves this problem, I want to give another illustrative thought exercise: have you ever played a game, and as you’re thinking about what move you could make, you also think about the various ways your opponent could respond to those moves? It’s common in chess, where you physically move a piece to a spot, and you examine the board carefully before taking your hand off the piece. Your goal is to make a good move, but simultaneously leave your opponent without any good retaliatory moves. This is the underlying principle of Minimax. It maximizes the score of your move, while minimizing the scores of your opponents possible retaliations. You can probably see where it got its name :-)
Now, you may be thinking “okay, but this suffers from the same problem”. That is, even if you think two moves ahead, and you’re playing moves that prevent your opponent from playing great moves, you may still be using a bad overall strategy and headed for destruction. This is especially true in a game like chess, where great players routinely sacrifice queens in order to adopt a superior overall strategy. If you’re just looking at the point values of such a game, the player with the better strategy who sacrificed a valuable piece is behind for a long period, but then towards the end of the game, when her strategy comes to fruition, she jumps ahead with a sudden checkmate, and her genius is revealed.
Minimax accounts for this by looking arbitrarily far ahead. Instead of just thinking two moves ahead, minimax can think 6 moves ahead, or 30 moves ahead. The more moves ahead, the better. In fact, the best case scenario is to simulate the entire rest of the game. The score of a node isn’t just the situation at the node, but it’s actually the score of the entire subtree underneath the node where every player has made their best possible move. The algorithm is limited only by computational power and time. But in a game like chess, where there are a total of 10^120 games that could be played, this is quite a limitation. To put this into perspective, if we tried a billion possibilities a second each move would take a trillion years at which point our opponent might start to get impatient. This is part of the reason why great chess players were still beating chess AIs until about 2006.
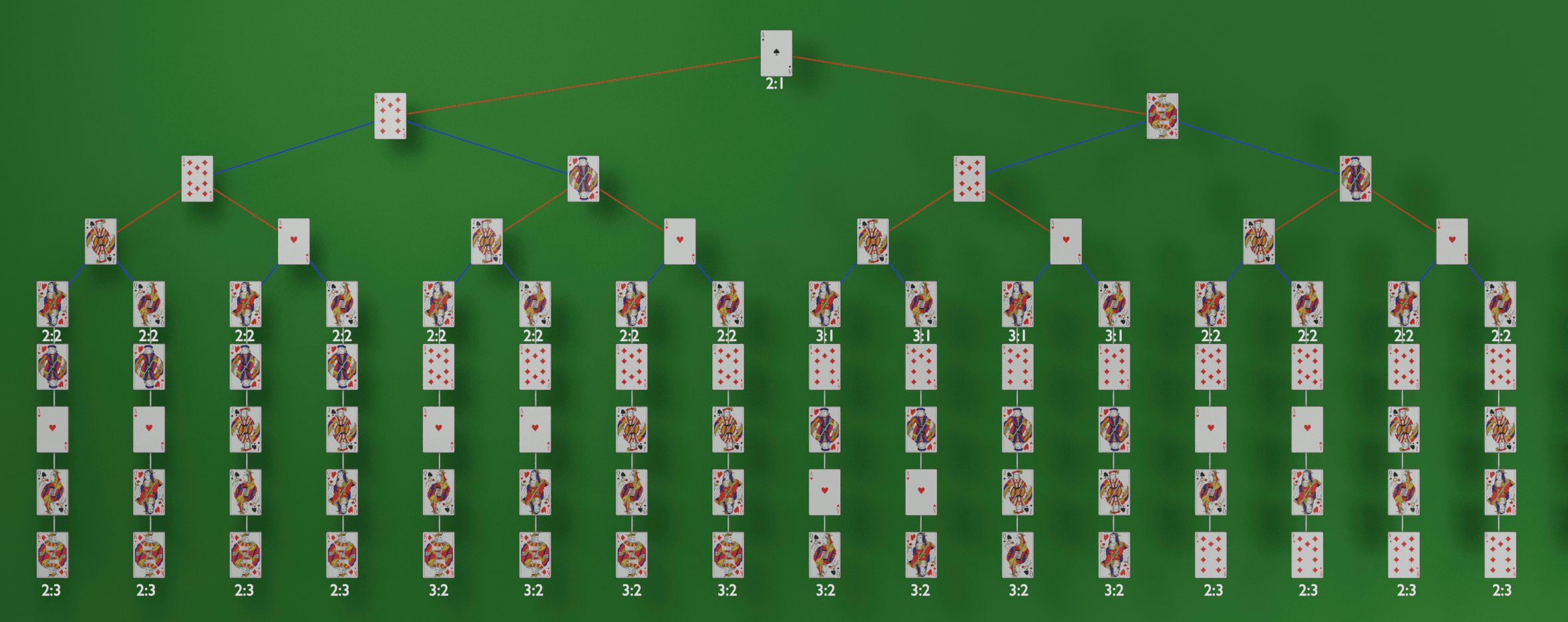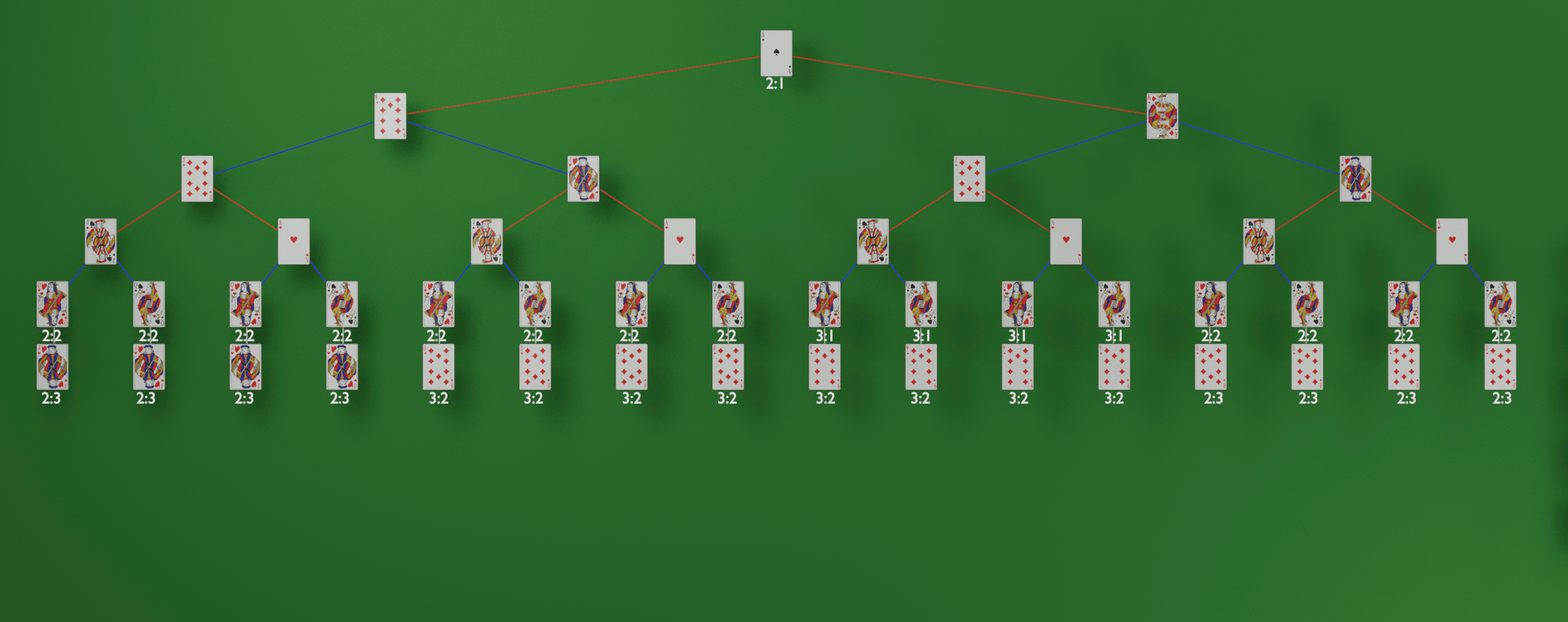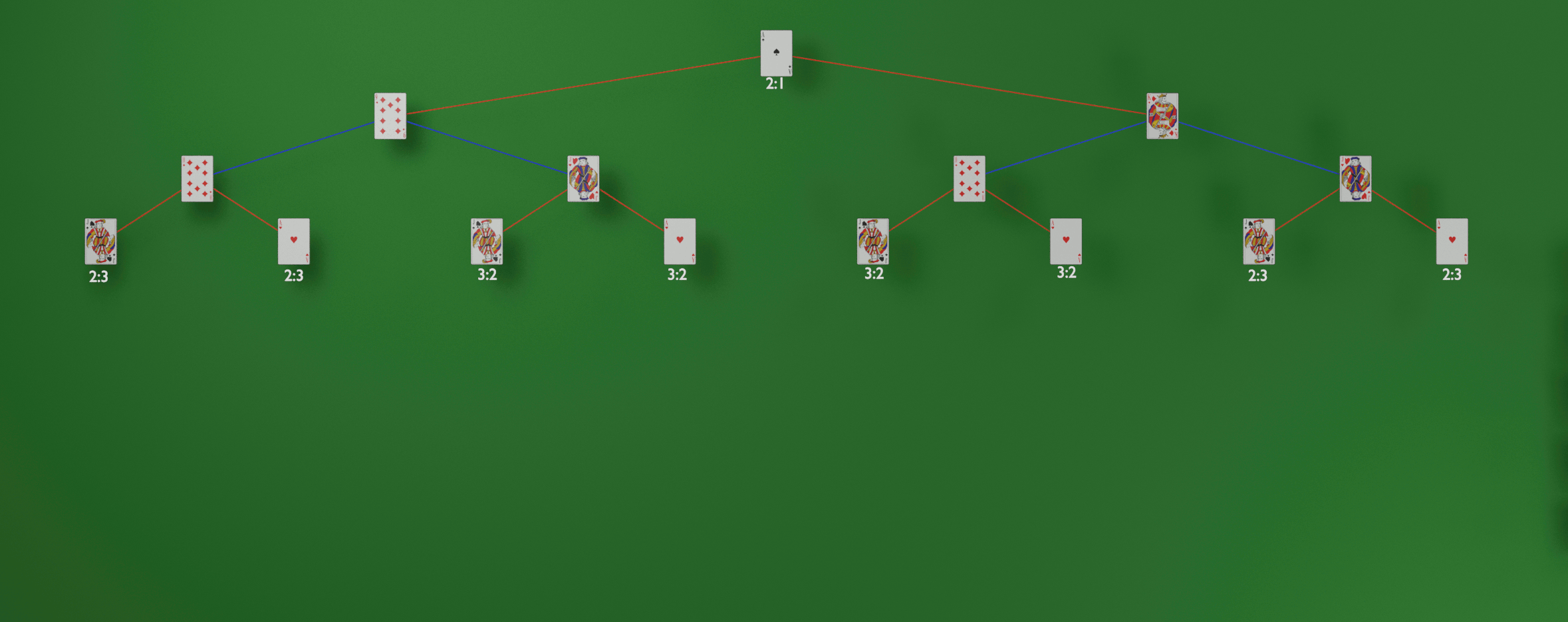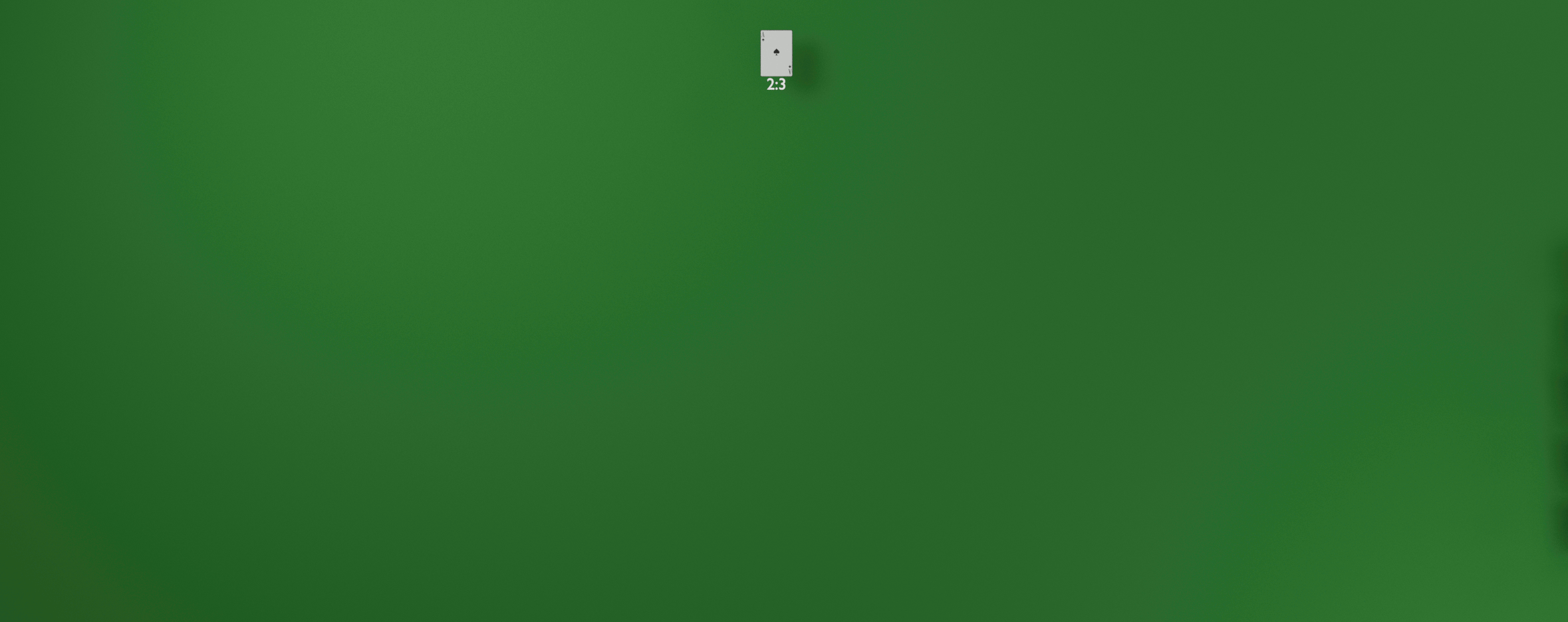
A Euchre game only has a teeny tiny fraction of the combinations of chess, so it’s actually fairly feasible to build the entire tree within an acceptable amount of time. That’s one of the reasons I chose Euchre for this series. As an example, here’s the full tree to represent our situation from above:
Yep, that’s every possible way the game could play out. We don’t have to look over this whole image right now, we’ll dig deep in a little bit, but I do want to call a few things out. The first thing is that it reads top to bottom. Each layer in the tree represents a move a player could make. You can see that the top three cards are A♠, 10♦, and J♥, representing the three possible moves that East could make. You can see that if the J♥ is played, the next row starts with a card from East’s hand. That’s because she won the trick by beating North’s Q♦ with the left bauer, so she gets to start the next trick. Conversely, when East plays the A♠, or 10♦, she loses the trick, and you can see the next layer starts with a card from North’s hand, because she wins with the Q♦. You might also wonder why the top of the tree has a bunch of branching, but towards the bottom it’s just a straight vertical line of cards. This is because it’s the end of the game and everyone only has a single card in their hand. They have to play that card, so there’s no branching. The branches represent choices players could make.
Speaking of choices, we as humans can probably see several fairly silly choices. For instance, East playing the 10♦ is probably a silly choice. Why would she throw away trump, and still lose the trick? We could potentially write a rule into our AI to prevent throwing away trump, and that way our algorithm could ignore that whole entire tree. That’s almost a third of the computation we would save.
This is a big part of writing an AI: coming up with such rules where you can prevent your AI from even thinking about objectively bad moves. These rules, in conjunction with a refined scoring algorithm, can cut down massively on the “decision space” that your AI has to consider. It can be a double edged sword, however, and you need to be an expert in the game sometimes to be able to tell that a move is objectively bad. After all, some moves (like sacrificing a queen), may look pretty bad, but can lead to unorthodox victories. We’ll speak a little about optimizing our AI decision space for our Euchre AI, but I don’t consider myself a Euchre expert, so we won’t get too deep into that.
Minimax In Depth
Okay, I still haven’t covered the details of how minimax works, so let’s go over that step by step.
Minimax constructs a tree out of every possible decision (exactly like our tree above). Each node represents a choice that a player can make, and the children of the node represent the choices of an opponent. In order to “score” a node, you choose the worst score from your children (worst from your perspective because you assume your opponent will pick the best decision). For example, if we define our score as north south tricks minus east west tricks, north south nodes will always pick the minimum value from their children and east west will pick the max. This process continues down to the bottom of the tree where there are no children. In that case, the actual trick difference, or score, is returned.
Okay, let’s go through each turn East could make. I mentioned earlier that the score in the game was 1:1 so far (that is, two tricks have already been played, and each team has one). First, let’s label scores. I’ll put scores next to every row that represents the end of a trick.
I know this is hard to read, we’ll zoom in in a minute.
Each branch represents a decision. If the decision is being made by north or south, she will favor the 3:2 outcomes. If a decision is being made by east or west, she will favor the 2:3 outcomes. Once we reach the last 5 rows, we’re locked in to whatever destiny our earlier turns led us to. We could actually collapse the last four rows and just slap the endgame score onto row 4, because at that point, there’s nothing anyone can do. We’ll talk about this a little later, but first, let’s discuss each play in detail.
A great example is the 10♦. Earlier, we mentioned that it might not be a great play. Let’s examine the 10♦ tree in isolation as an example:
You can see that every single outcome is 3:2, meaning north south wins. So, if East chooses 10♦, her team loses no matter what. It’s a foregone conclusion. Therefore, she shouldn’t choose that play.
Now let’s examine the left bauer:
This is more complex, as the outcomes differ depending on how the game plays out. However, let’s look at the same image, but label each decision based on which team is making it. I’ll use red for north south, and blue for east west, and white for if there’s no decision (i.e. only one valid play exists):
Now look at the last row before fate is sealed. It’s the fourth row from the top. That last decision is a north south decision, and if you look at the bottom of all of those columns, there is always a 3:2 option. This is obviously the option that the player would choose, so therefore, if we pick the left bauer, we lose the game unless our opponent makes a terrible blunder. And I can tell you right now, if you’re hoping a grandma will make a blunder during a card game, you might as well pack your bags right now and get out of town.
Again, you could collapse everything up until the fourth row and label it as 3:2, because that player will obviously pick moves that lead to that outcome, and if that’s the case, we’re in a similar spot as we were with our 10♦, where every possible outcome was a loss. This is how I like to think of minimax sometimes: you label your leaf nodes and collapse upward. When there are branches, you choose the best outcome for the deciding player as you merge it into one outcome. At the end of this process, you’re left with an outcome for all your potential moves and you just pick the best one.
Alright, let’s check out the last turn:
This time, let’s calculate the score with Minimax. We’ll start at the bottom and collapse upward. Every red decision will pick a better outcome for north south, and every blue decision will pick a better outcome for east west.
You can see that the game comes down to a decision on the third row. If East plays the A♠ and loses, North will follow up with either the K♦ or the 9♦. At this point, East has control of the game. If she plays the higher trump to beat the K♦ or 9♦, she’ll win the game.
So, in this scenario, we had to think at least 3 moves ahead in order to definitively tell which play would win the game, but this is an end-game scenario. Imagine the beginning of the game, where the branching factor is orders of magnitude more complicated! Luckily, Minimax can apply these same rules we’ve discussed to arbitrarily deep trees, so you’ll see that it’s not a problem at all. We can just sit back, relax, and let the computer do all the work.
Conclusion
Minimax is an incredibly powerful algorithm that’s applicable to countless games. It is the grandfather of many AI algorithms in use today. We’ve discussed it in detail in this chapter to get a basic idea of how the algorithm functions. In the next chapter, we’ll implement a version in our flutter application and experience the pleasure of losing to it repeatedly!
Thanks David Bellot for the great card graphics!